A Morpho-Recursive Function for Pi
I'm working on building a little video (still!) to explain how I came up with a method that borrows a bit from recursive function theory to build a method for generating pi by iteratively building a recursive method, which morphs at first, and then eventually stabilizes to generate an n sided polygon.
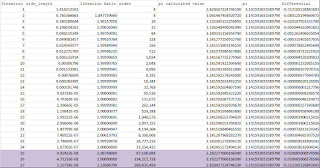
As each iteration goes forth, n increases, doubling the number of sides of an n-sided polygon, until the sides get so small that it "smooths" out the perception of a circle - which is interesting because after the 5th iteration, the function "stabilizes", and smooths out, making the incremental change between values of pi get smaller, but pi itself gets more precise to the "true" value of pi itself.
The problem with this method computationally is that computers start "blowing up" because the sides approach a value of 0, but cannot actually get there. But, from a computer's point of view, these sides might as well be zero. The sides cannot obviously have a side length of zero. But, they can get really, really, really small and one will eventually see there are repeating structures in the construction of the algorithm.
Here's an interesting Excel Sheet that shows what goes on:
I'll also provide some sheets/drawings along with the video (work in progress) so that people can see how this was all derived. It's nothing difficult beyond high school algebra. But the cool thing is that what is used to help calculate the value of pi can be plugged back into itself to generate these values for pi.
Iteration 27: Notice how the value of Pi becomes equal to the value of pi at iteration 1! It returns itself to the first iteration value! Spooky stuff. But, again, that has to do with the computer's issues in calculating very small floating-point numbers.
As each iteration goes forth, n increases, doubling the number of sides of an n-sided polygon, until the sides get so small that it "smooths" out the perception of a circle - which is interesting because after the 5th iteration, the function "stabilizes", and smooths out, making the incremental change between values of pi get smaller, but pi itself gets more precise to the "true" value of pi itself.
The problem with this method computationally is that computers start "blowing up" because the sides approach a value of 0, but cannot actually get there. But, from a computer's point of view, these sides might as well be zero. The sides cannot obviously have a side length of zero. But, they can get really, really, really small and one will eventually see there are repeating structures in the construction of the algorithm.
Here's an interesting Excel Sheet that shows what goes on:
I'll also provide some sheets/drawings along with the video (work in progress) so that people can see how this was all derived. It's nothing difficult beyond high school algebra. But the cool thing is that what is used to help calculate the value of pi can be plugged back into itself to generate these values for pi.
Iteration 27: Notice how the value of Pi becomes equal to the value of pi at iteration 1! It returns itself to the first iteration value! Spooky stuff. But, again, that has to do with the computer's issues in calculating very small floating-point numbers.
What would the post be without pictures?
Enjoy. A sort of window into my mind.


Comments
Post a Comment